暗号化のお話 (2)
| 前へ << 暗号化のお話 (1) | 暗号化のお話 (3) >> 次へ |
共通鍵の弱点を克服
初対面の 2人の間で鍵の受け渡しが安全にできない、 という共通鍵の弱点を克服したのが「公開鍵暗号方式」です。この方式は公開鍵と秘密鍵という 2つの鍵を使います。
- 秘密鍵で暗号化したデータは公開鍵で復号できます
(秘密鍵で暗号化したデータは公開鍵を使わないと復号できません)。 - 公開鍵で暗号化したデータは秘密鍵で復号できます
(公開鍵で暗号化したデータは秘密鍵を使わないと復号できません)。
秘密鍵は文字どおり秘密にしておきます。自分しか知らない鍵です。 公開鍵は文字どおり公開しても構いません。というより、 積極的に宣伝してもよいです。web に公開鍵を置いても、 新聞広告に公開鍵を載せても構いません。
公開鍵方式での暗号化
最初の状態を図 1 に示します。- 送信者は受信者とネットワーク経由で初めて出会った
- 送信者は受信者に平文を送りたい
- 誰が盗聴しているかわからないので、ネットワーク経由で共通鍵を渡すことはできない。
- 受信者は、公開鍵を公開している。秘密鍵は受信者しか知らない。
 |
| 図 1: 公開鍵暗号方式の初期状態 |
さてここで、図 2 のような手順でデータをやりとりします。
- 送信者は相手 (受信者) の公開鍵を取り寄せます。
- 送信者は取り寄せた公開鍵でデータを暗号化し、暗号文を送信します。
- 受信者は、自分の秘密鍵でデータを復号し、平文を手に入れます。
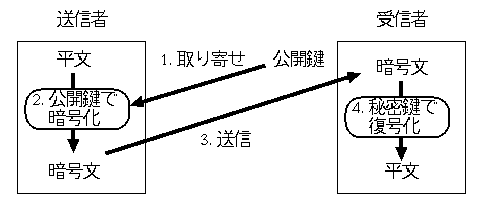 |
| 図 2: 公開鍵暗号方式の流れ |
- 受信者の公開鍵
- 公開鍵で暗号化した平文
ここで説明したやりかたで、確かに安全に暗号化を実現することができます。 ただし公開鍵暗号方式の中で最も広く使われている RSA という暗号方式は、 暗号化・復号化に非常に時間がかかるという欠点があります。 どれくらい遅いかというと、一般的な共通鍵方式の数百〜千倍遅いのです。
実際の暗号化処理
公開鍵方式が遅いのなら (正確には公開鍵方式のひとつである RSA が遅い)、 処理速度が速い共通鍵を使って暗号化すればよいのです。 しかし共通鍵をそのまま送信すると、共通鍵を盗聴されてしまいます。 そのジレンマを解決するのが、「共通鍵を公開鍵方式を用いて暗号化する」 という方式です。具体的には図 3 のような流れになります。
- 送信者は相手 (受信者) の公開鍵を取り寄せます。
- 送信者は共通鍵を生成し、平文を共通鍵で暗号化します。 共通鍵で暗号化していますので、暗号化に要する時間は短くて済みます。
- 送信者は生成した共通鍵を、取り寄せた公開鍵で暗号化します。 共通鍵の長さはせいぜい数十〜数百ビット程度なので、 遅い公開鍵方式で暗号化したところでそれほど時間はかかりません。
- 送信者は「暗号文と、公開鍵で暗号化した共通鍵」を送信します。
- 受信者は、受信した「公開鍵で暗号化した共通鍵」を秘密鍵で復号化します。
- 受信者は、受信した暗号文を、復号化した共通鍵で復号化します。 これで平文が取り出せました。
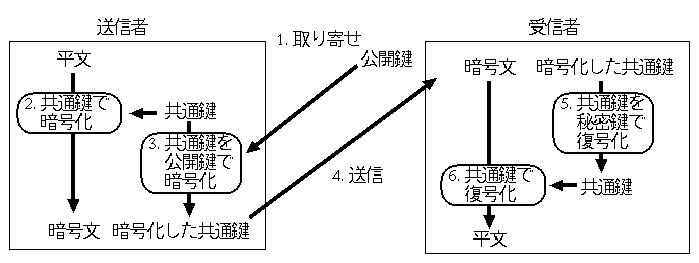 |
| 図 3: 公開鍵暗号方式と共通鍵暗号方式の組合せ |
- 平文を鍵 (共通鍵) を用いて暗号化すること。
- その鍵 (共通鍵) をさらに別の鍵 (公開鍵) で暗号化すること。
- 受信者の公開鍵
- 受信者の秘密鍵
- 送信者が生成した共通鍵
もしネットワークが盗聴されていたとして、盗聴者が手に入れられるものは
- 受信者の公開鍵
- 共通鍵で暗号化した平文
- 公開鍵で暗号化した共通鍵
公開鍵暗号方式の正体は?
「暗号化と復号化のときに使用する鍵が異なる」というのは、よく考えてみれば不思議なことです。 身の回りにそのような鍵はあるでしょうか?共通鍵方式の「暗号化と復号化で同じ鍵を使う」というのは身の回りにありふれています。 たとえば家の鍵も金庫の鍵も、鍵は 1つ、つまり共通鍵方式です。 しかし、施錠と開錠で異なる鍵を使うような金庫はありません。 2000年以上の暗号史上、鍵といえば共通鍵だったのです。
しかし 1977年、MIT の Ronald Rivest、Adi Shamir、Len Adleman の 3人が 「暗号化と復号化のときに別の鍵を使う」という暗号方式を考え出しました。 この公開鍵暗号方式を、3人の名前の頭文字をとって「RSA」と言います。
RSA が利用したのは「素数」です。
ある大きな数、たとえば 2149673006040161867 を素因数分解するにはとてつもない時間がかかります。 この 2149673006040161867 を公開鍵とします。 実は上記の数は素数である 1938918661 と 1108696847 をかけたものですが、 この 2つの数を秘密鍵とします。
確かに 2149673006040161867 を地道に計算すれば、いつかは 1938918661 と 1108696847 に たどり着きます。しかし、それに要する時間はとてつもなく大きいものです。
RSA の本当のところ
実際に RSA で暗号化と復号化をしてみましょう。 当ページ管理人は数式が嫌いなので、さらっと流します。まず、素数を 2つ求めます。ここでは
p = 17, q = 23としましょう。次に n を求めます。n は p * q です。
n = p * q = 17 * 23 = 391次に L を求めます。L は (p-1) と (q-1) の最小公倍数です。
L = (17-1) と (23-1) の最小公倍数 = 16 と 22 の最小公倍数 = 176次に e を求めます。e は e と L との最大公約数が 1 となる数です (つまり互いに素である数)。e はたくさん候補が見付かります。
e = 3, 5, 7, 13, 17, ...ここでは e = 13 を選択します。
ここまでで、e = 13, n = 391 という結果が得られました。実はこれが公開鍵です。 公開鍵は、2つの数のペアなのです。
次に d を求めます。d は「(e * d) % L = 1」となる数です。d もたくさんの数が見付かります。
d = 149, 325, 501, ...ただし d は 1<d<L を満たす必要があるので d=149 となります。
これで d = 149, n = 391 という結果が得られました。これが秘密鍵です。 秘密鍵も 2つの数のペアなわけです。 まとめると、
- 公開鍵は e と n です。つまり 13 と 391 です。
- 秘密鍵は d と n です。つまり 149 と 391 です。
暗号文 = (平文^e) % n = (97^13) % 391 = 320となり、暗号文は 320 となります (97 の 13 乗なんて計算していられないので、bc コマンドでさっくり計算してください)。 今度は 320 を復号化してみましょう。 RSA における復号化とは、(暗号文^d) % n を計算することです。
平文 = (暗号文^d) % n = (320^149) % 391 = 97ちゃんと平文と同じ 97 が得られました。
この例では e を選択しましたが、e と L が互いに素であればよいので、 e に常に固定の値を使うようにしても問題ありません。 例えば現実の実装では 3, 17, 65537 がよく使われます。 なぜこれらの数か、という理由は以下の通り。
- 小さい数であること。暗号化の際には平文を e 乗するわけなので、 e の数が小さければ小さいほど暗号化処理が高速になる。 なお、e の数が小さくても解読されやすいわけではない (一方、復号化の際は d 乗するが、この d が小さいと解読されやすい)。
- ビットがあまり立っていないこと。3, 17, 65537 を 2進数で書くと、それぞれ 11, 10001, 10000000000000001 となる。 詳細は省略するが、ビットが立っていないほど e 乗の処理が高速になる
RSA と素因数分解
RSA の安全性の根拠は「大きな数の素因数分解が難しい」ということです。 ただし、それが数学的に証明されているわけではありません。 明日になれば、誰かが素因数分解を 1秒で行える方法を考案するかもしれません。 もしそうなれば、明日から RSA は無力です。RSA が公表された 1977年、雑誌に RSA の紹介記事が載りました。その問題がこれです。
| 1143816257578888676 | |
| 9007 | |
| 1066986143685780244 |
この問題は n が 10進数で 129 桁であることから、RSA-129 と呼ばれました。 「暗号技術大全」には
1977年、Ron Rivest は 125 桁の数を因数分解するのに 4京 (40,000兆) 年かかると言った。とありますので、この問題を作成した Ron Rivest は RSA-129 は永遠に解読できないと思っていたのかもしれません。
しかし 1994年、1600台のマシンを用いて 129桁の n が素因数分解され、RSA-129 が 解読されました。 解読された理由は、コンピュータが著しく高速化したことと、 インターネットによって多くのコンピュータの参加が可能になったこと、です。
さらに、素因数分解のアルゴリズムは日々改善されています。
- 2次ふるい法 (QS = Quadratic Sieve)
- 複数多項式 2次ふるい法 (MPQS = Multiple Polynomial Quadratic Sieve)
- 数体ふるい法 (NFS = Number Field Sieve)
- 一般数体ふるい法 (GNFS = General Number Field Sieve)
RSA Security 社が素因数分解のコンテスト RSA Factoring Challenge を開催しています。 2003年12月現在、RSA-140・RSA-155・RSA-160・RSA-576・RSA-640 は既に解かれ、RSA-1024 〜 RSA-2048 が未解読です。 素因数分解に成功すると bit 長に応じた賞金がもらえます。例えば RSA-2048 だと賞金は 20万ドルです (RSA-160 までの RSA-XXX の XXX は、10進数での桁数を表していましたが、 RSA-576 以降は 2進数でのビット数を表すようになりました)。
| チャレンジ名 | ビット数 | 終了時期 |
|---|---|---|
| RSA-129 | 428bit | 1994年4月27日 |
| RSA-140 | 466bit くらい | 1999年2月2日 |
| RSA-155 | 512bit | 1999年8月22日 |
| RSA-160 | 530bit | 2003年4月1日 |
| RSA-576 | 576bit・10進数で 174桁 | 2003年12月3日 |
| RSA-640 | 640bit・10進数で 193桁 | 2005年11月2日 解読者のメール |
| RSA-1024 | 1024bit・10進数で 309桁 | 未解決 |
| RSA-2048 | 2048bit・10進数で 617桁 | 未解決 |
RSA の鍵長はどの程度にするのがよいのでしょうか? 2003年12月時点では「最低でも 1024 bit」という評価が適当であろうと思います。 ちなみに OpenSSL-0.9.7c で RSA 鍵を生成した場合、鍵長を指定しない場合のデフォルトは 512 bit 鍵です。これは短すぎるので、最低でも 1024 bit を指定するようにしましょう。
でも、1024 bit 鍵はいつまで安全なのでしょうか? ふたたび「暗号技術大全」から引用します。
大きな数の因数分解は難しい。しかしアルゴリズム設計者にとっては不幸なことに、 どんどん簡単になってきている。もっと不幸なことに、 数学者が予想したより速く簡単になりつつある。 1976年、Richard Guy は 「今世紀中にだれかが 10^80 規模の数を普通に因数分解するようになったら驚きだ」 と書いた。1977年、Ron Rivest は 125 桁の数を因数分解するのに 4京 (40,000兆) 年かかると言った。1994年に 129 桁の数が因数分解された。 このことに何か教訓があるとすれば、予測なんかするもんじゃないよ、ということだ。
| 前へ << 暗号化のお話 (1) | 暗号化のお話 (3) >> 次へ |
ご意見・ご指摘は Twitter: @68user までお願いします。